Counting Sort §

1. Find out the maximum element (let it be max) from the given array.

2. Initialize an array of length max+1 with all elements 0. This array is used for storing the count of the elements in the array.

3. Store the count of each element at their respective index in count array For example: if the count of element 3 is 2 then, 2 is stored in the 3rd position of count array. If element “5” is not present in the array, then 0 is stored in 5th position.

4. Store cumulative sum of the elements of the count array. It helps in placing the elements into the correct index of the sorted array.

5. Find the index of each element of the original array in the count array. This gives the cumulative count. Place the element at the index calculated as shown in figure below.

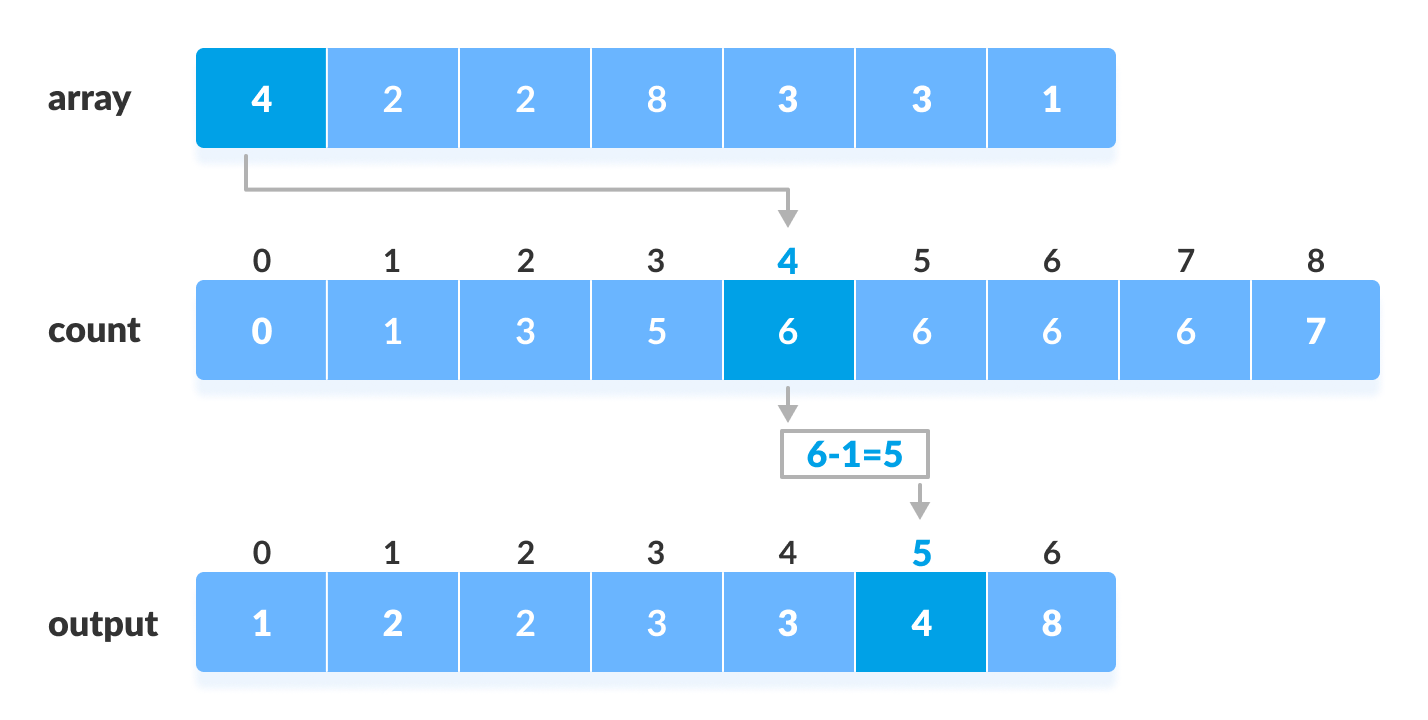
6. After placing each element at its correct position, decrease its count by one.

Implementation §

def countingSort(array):
    size = len(array)
    output = [0] * size
 
    # Initialize count array
    count = [0] * 10
 
    # Store the count of each elements in count array
    for i in range(0, size):
        count[array[i]] += 1
 
    # Store the cummulative count
    for i in range(1, 10):
        count[i] += count[i - 1]
 
    # Find the index of each element of the original array in count array
    # place the elements in output array
    i = size - 1
    while i >= 0:
        output[count[array[i]] - 1] = array[i]
        count[array[i]] -= 1
        i -= 1
 
    # Copy the sorted elements into original array
    for i in range(0, size):
        array[i] = output[i]
 
 
data = [4, 2, 2, 8, 3, 3, 1]
countingSort(data)
print(data)

Complexity §

Stability: Yes

Space Complexity §

The space complexity of Counting Sort is O(max). Larger the range of elements, larger is the space complexity.

Time Complexity §

There is no comparison between any elements, so it is better than comparison based sorting techniques. But, it is bad if the integers are very large because the array of that size should be made.

Worst Case Complexity: O(n+k) Best Case Complexity: O(n+k) Average Case Complexity: O(n+k)

In all the above cases, the complexity is the same because no matter how the elements are placed in the array, the algorithm goes through n+k times.

Reference §

https://www.youtube.com/watch?v=7zuGmKfUt7s https://rust-algo.club/sorting/counting_sort/