Search

SearchSearch

Dec 13, 2025, 5 min read

Merge Sort

Merge sort uses a divide and conquer strategy.

Suppose we had to sort an array A. A subproblem would be to sort a sub-section of this array starting at index p and ending at index r, denoted as A[p..r].

Divide

If q is the half-way point between p and r, then we can split the subarray A[p..r] into two arrays A[p..q] and A[q+1, r].

Conquer

In the conquer step, we try to sort both the subarrays A[p..q] and A[q+1, r]. If we haven’t yet reached the base case, we again divide both these subarrays and try to sort them.

Combine

When the conquer step reaches the base step and we get two sorted subarrays A[p..q] and A[q+1, r] for array A[p..r], we combine the results by creating a sorted array A[p..r] from two sorted subarrays A[p..q] and A[q+1, r].

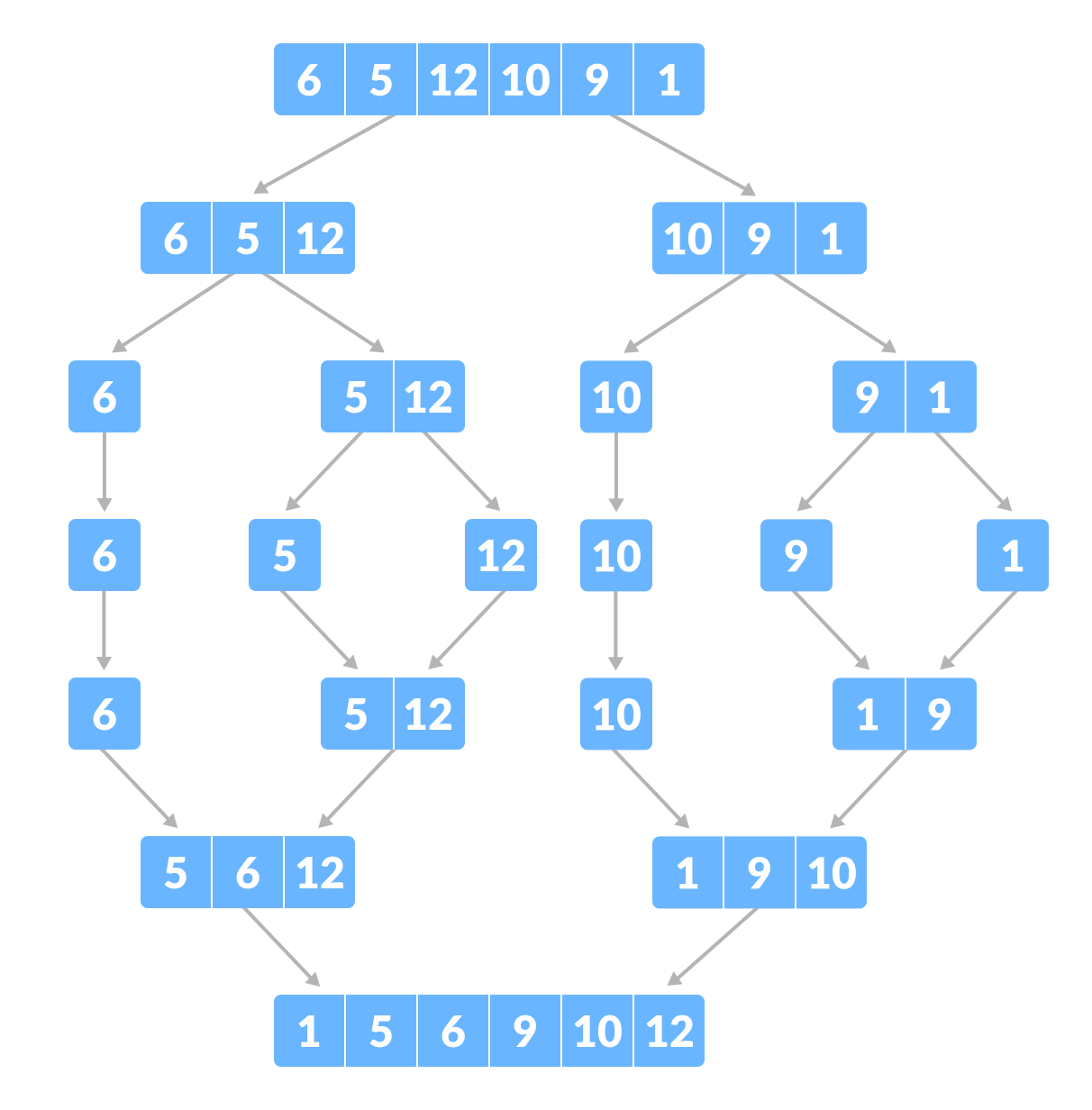
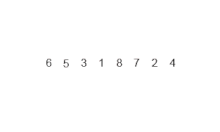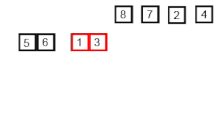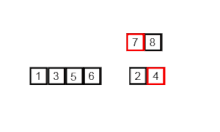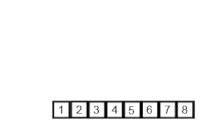
The merge Step of Merge Sort

The merge step is the solution to the simple problem of merging two sorted lists(arrays) to build one large sorted list(array).

The algorithm maintains three pointers, one for each of the two arrays and one for maintaining the current index of the final sorted array.

Have we reached the end of any of the arrays?
    No:
        Compare current elements of both arrays 
        Copy smaller element into sorted array
        Move pointer of element containing smaller element
    Yes:
        Copy all remaining elements of non-empty array

The merge function works as follows:

  1. Create copies of the subarrays L <- A[p..q] and M <- A[q+1..r].

  2. Create three pointers i, j and k i maintains current index of L, starting at 1 j maintains current index of M, starting at 1 k maintains the current index of A[p..q], starting at p.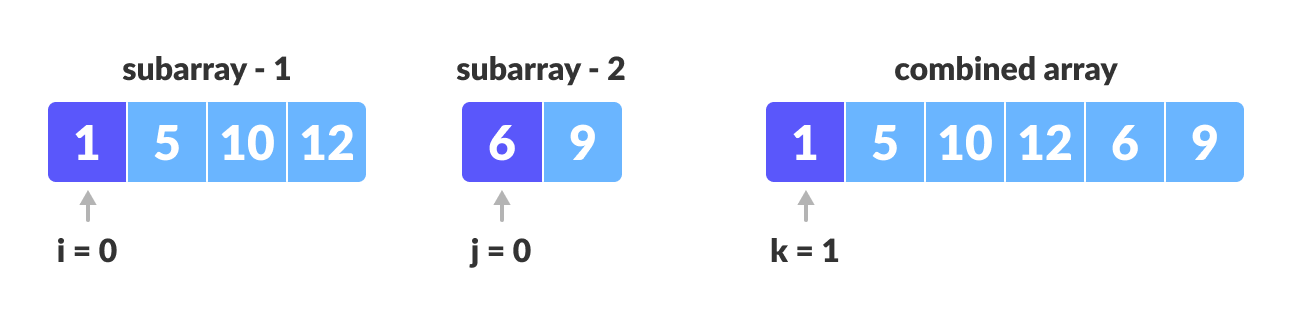

  3. Until we reach the end of either L or M, pick the larger among the elements from L and M and place them in the correct position at A[p..q]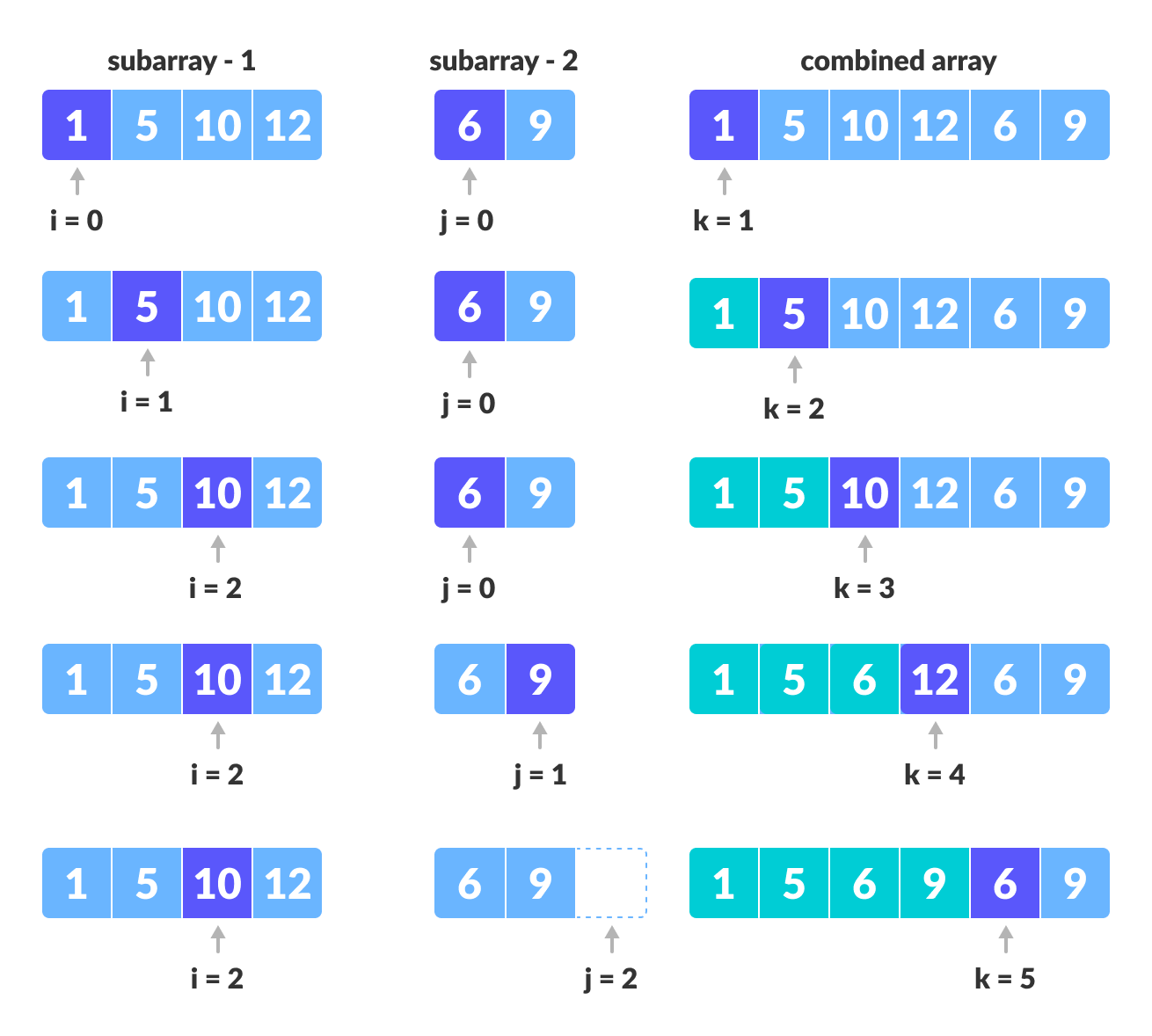

  4. When we run out of elements in either L or M, pick up the remaining elements and put in A[p..q]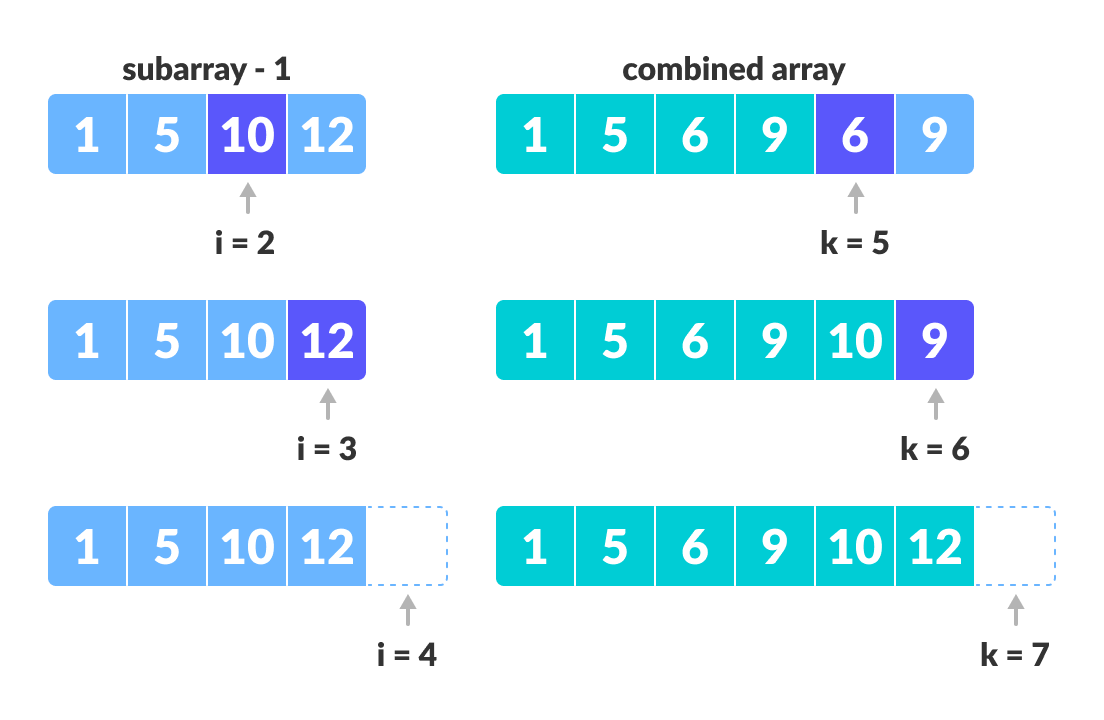

Implementation

var merge = function (array, p, q, r) {
  var lowHalf = [];
  var highHalf = [];
  var k = p;
  var i;
  var j;
 
  for (i = 0; k <= q; i++, k++) {
    lowHalf[i] = array[k];
  }
 
  for (j = 0; k <= r; j++, k++) {
    highHalf[j] = array[k];
  }
 
  k = p;
  i = 0;
  j = 0;
  while (i < lowHalf.length && j < highHalf.length) {
    if (lowHalf[i] < highHalf[j]) {
      array[k] = lowHalf[i];
      i++;
    } else {
      array[k] = highHalf[j];
      j++;
    }
    k++;
  }
  while (i < lowHalf.length) {
    array[k] = lowHalf[i];
    i++;
    k++;
  }
  while (j < highHalf.length) {
    array[k] = highHalf[j];
    j++;
    k++;
  }
};
 
var mergeSort = function (array, p, r) {
  if (r > p) {
    var q = Math.floor((r + p) / 2);
    mergeSort(array, p, q);
    mergeSort(array, q + 1, r);
    merge(array, p, q, r);
  }
};
public static void sort(Comparable[] a) {
  aux = new Comparable[a.length];
  sort(a, aux, 0, a.length - 1);
}
 
private static void sort(Comparable[] a, Comparable[] aux, int lo, int hi) {
  if (hi <= lo)
    return;
  int mid = lo + (hi - lo) / 2;
  sort(a, aux, lo, mid);
  sort(a, aux, mid + 1, hi);
  merge(a, aux, lo, mid, hi);
}
 
private static void merge(Comparable[] a, Comparable[] aux, int lo, int mid, int hi) {
  for (int k = lo; k <= hi; k++)
    aux[k] = a[k];
  int i = lo, j = mid + 1;
  for (int k = lo; k <= hi; k++) {
    if (i > mid)
      a[k] = aux[j++];
    else if (j > hi)
      a[k] = aux[i++];
    else if (less(aux[j], aux[i]))
      a[k] = aux[j++];
    else
      a[k] = aux[i++];
  }
}
def mergeSort(array):
    if len(array) > 1:
        #  r is the point where the array is divided into two subarrays
        r = len(array)//2
        L = array[:r]
        M = array[r:]
 
        # Sort the two halves
        mergeSort(L)
        mergeSort(M)
 
        i = j = k = 0
 
        # Until we reach either end of either L or M, pick larger among
        # elements L and M and place them in the correct position at A[p..r]
        while i < len(L) and j < len(M):
            if L[i] < M[j]:
                array[k] = L[i]
                i += 1
            else:
                array[k] = M[j]
                j += 1
            k += 1
 
        # When we run out of elements in either L or M,
        # pick up the remaining elements and put in A[p..r]
        while i < len(L):
            array[k] = L[i]
            i += 1
            k += 1
 
        while j < len(M):
            array[k] = M[j]
            j += 1
            k += 1
 
# Print the array
def printList(array):
    for i in range(len(array)):
        print(array[i], end=" ")
    print()
 
# Driver program
if __name__ == '__main__':
    array = [6, 5, 12, 10, 9, 1]
 
    mergeSort(array)
 
    print("Sorted array is: ")
    printList(array)

Merge Sort Complexity

Space Complexity: O(n) Stability: Yes

Time Complexity

In the divide stage, the entire array will be divided into minimum sub-arrays (equal or fewer than 2 elements), which will then be sorted using simple comparison. the time complexity for this stage is O(log(n))

In the conquer stage, the adjacent sub-arrays will be merged together, the time complexity for this stage is O(n)

Hence the time complexity for the entire algorithm is O(n*log(n))

Best O: (n*log n) Worst O: (n*log n) Average: O(n*log n)

Reference

Merge Sort (With Code in Python/C++/Java/C)

Backlinks