Heap Sort Heapify §

Starting from a complete binary tree, we can modify it to become a Max-Heap by running a function called heapify on all the non-leaf elements of the heap.

Base case §

Since heapify uses recursion, it can be difficult to grasp. So let’s first think about how you would heapify a tree with just three elements.

heapify(array)
    Root = array[0]
    Largest = largest( array[0] , array [2*0 + 1]. array[2*0+2])
    if(Root != Largest)
          Swap(Root, Largest)

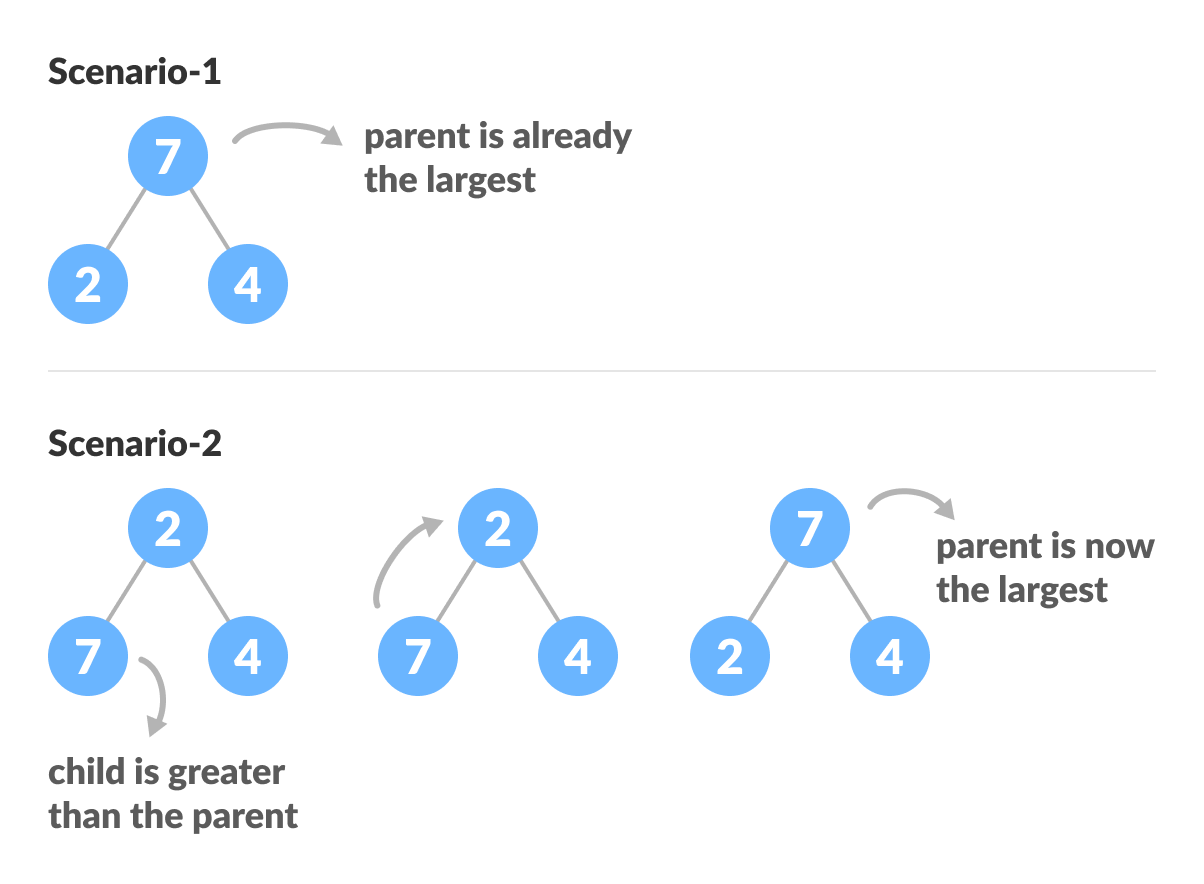
The example above shows two scenarios - one in which the root is the largest element and we don’t need to do anything. And another in which the root had a larger element as a child and we needed to swap to maintain max-heap property.

If you’re worked with recursive algorithms before, you’ve probably identified that this must be the base case.

Multiple levels §

Now let’s think of another scenario in which there is more than one level. 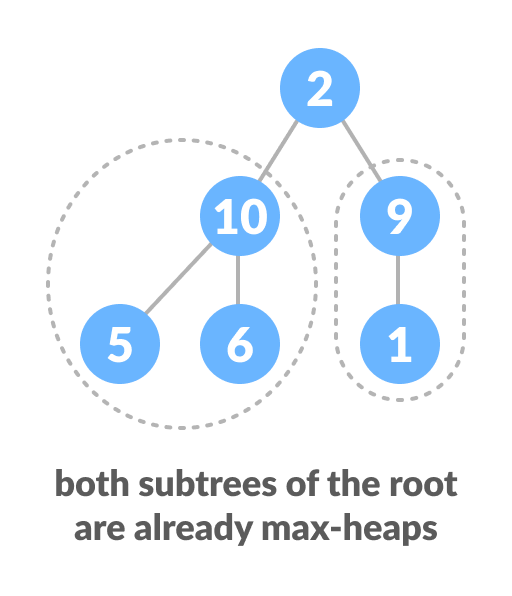The top element isn’t a max-heap but all the sub-trees are max-heaps.

To maintain the max-heap property for the entire tree, we will have to keep pushing 2 downwards until it reaches its correct position.

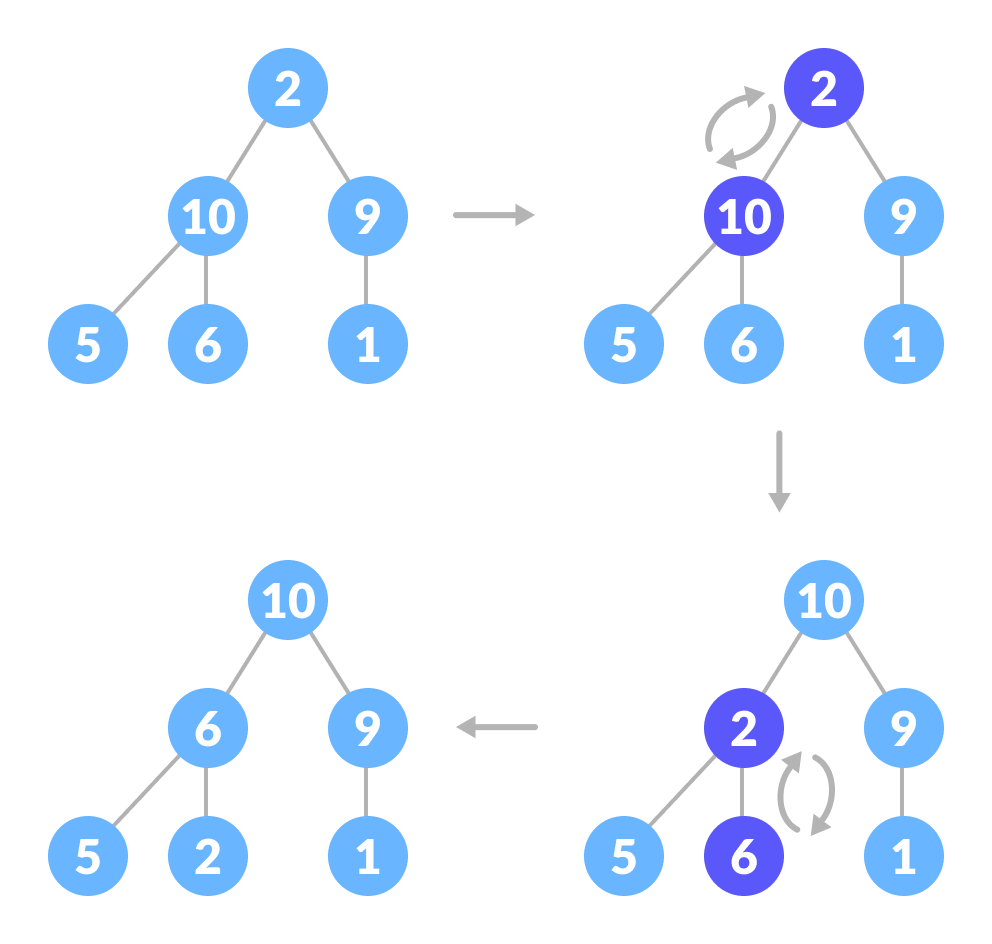
Thus, to maintain the max-heap property in a tree where both sub-trees are max-heaps, we need to run heapify on the root element repeatedly until it is larger than its children or it becomes a leaf node.

We can combine both these conditions in one heapify function as

void heapify(int arr[], int n, int i) {
  // Find largest among root, left child and right child
  int largest = i;
  int left = 2 * i + 1;
  int right = 2 * i + 2;
 
  if (left < n && arr[left] > arr[largest])
    largest = left;
 
  if (right < n && arr[right] > arr[largest])
    largest = right;
 
    // Swap and continue heapifying if root is not largest
    if (largest != i) {
      swap(&arr[i], &arr[largest]);
      heapify(arr, n, largest);
  }
}

This function works for both the base case and for a tree of any size. We can thus move the root element to the correct position to maintain the max-heap status for any tree size as long as the sub-trees are max-heaps.

General scenario (Build max-heap) §

To build a max-heap from any tree, we can thus start heapifying each sub-tree from the bottom up and end up with a max-heap after the function is applied to all the elements including the root element.

In the case of a complete tree, the first index of a non-leaf node is given by n/2 - 1. All other nodes after that are leaf-nodes and thus don’t need to be heapified.

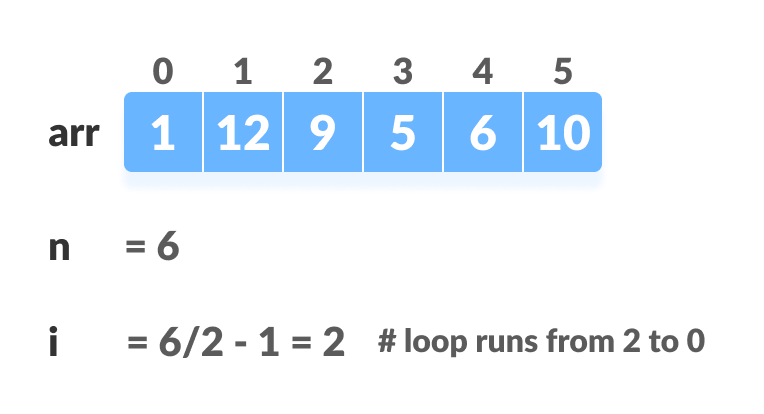So, we can build a maximum heap as

// Build heap (rearrange array)
for (int i = n / 2 - 1; i >= 0; i--)
  heapify(arr, n, i);

i = 2 §

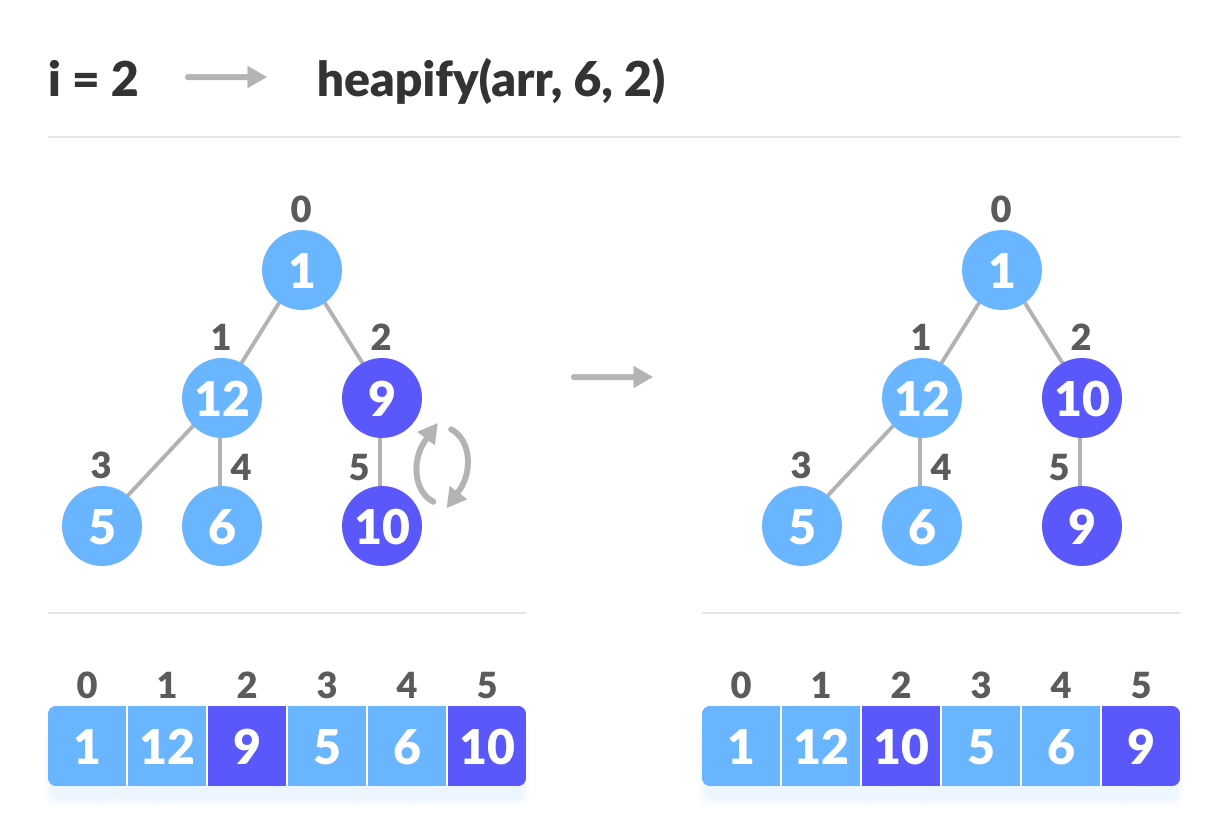
i = 1 §

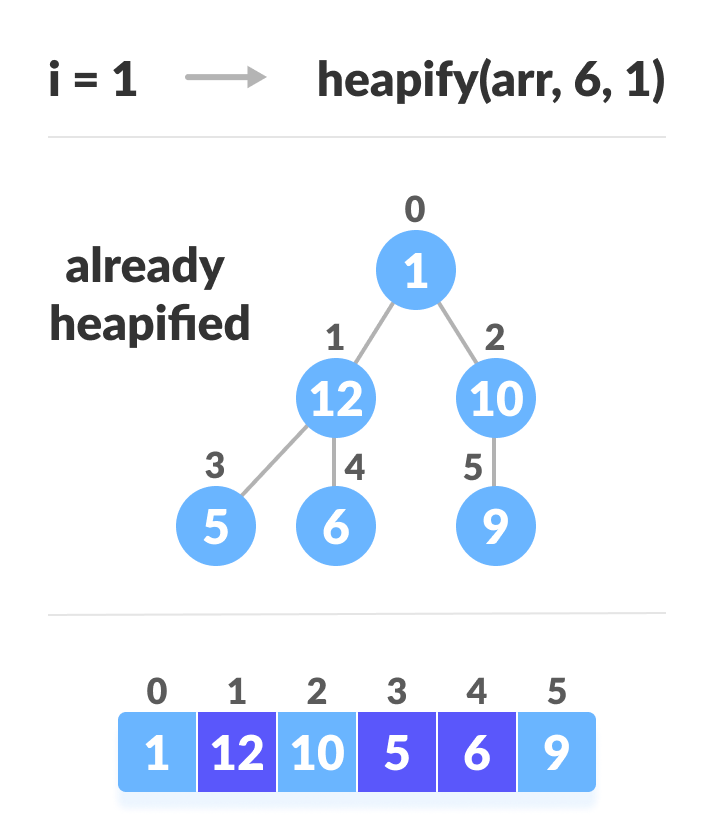
i = 0 §

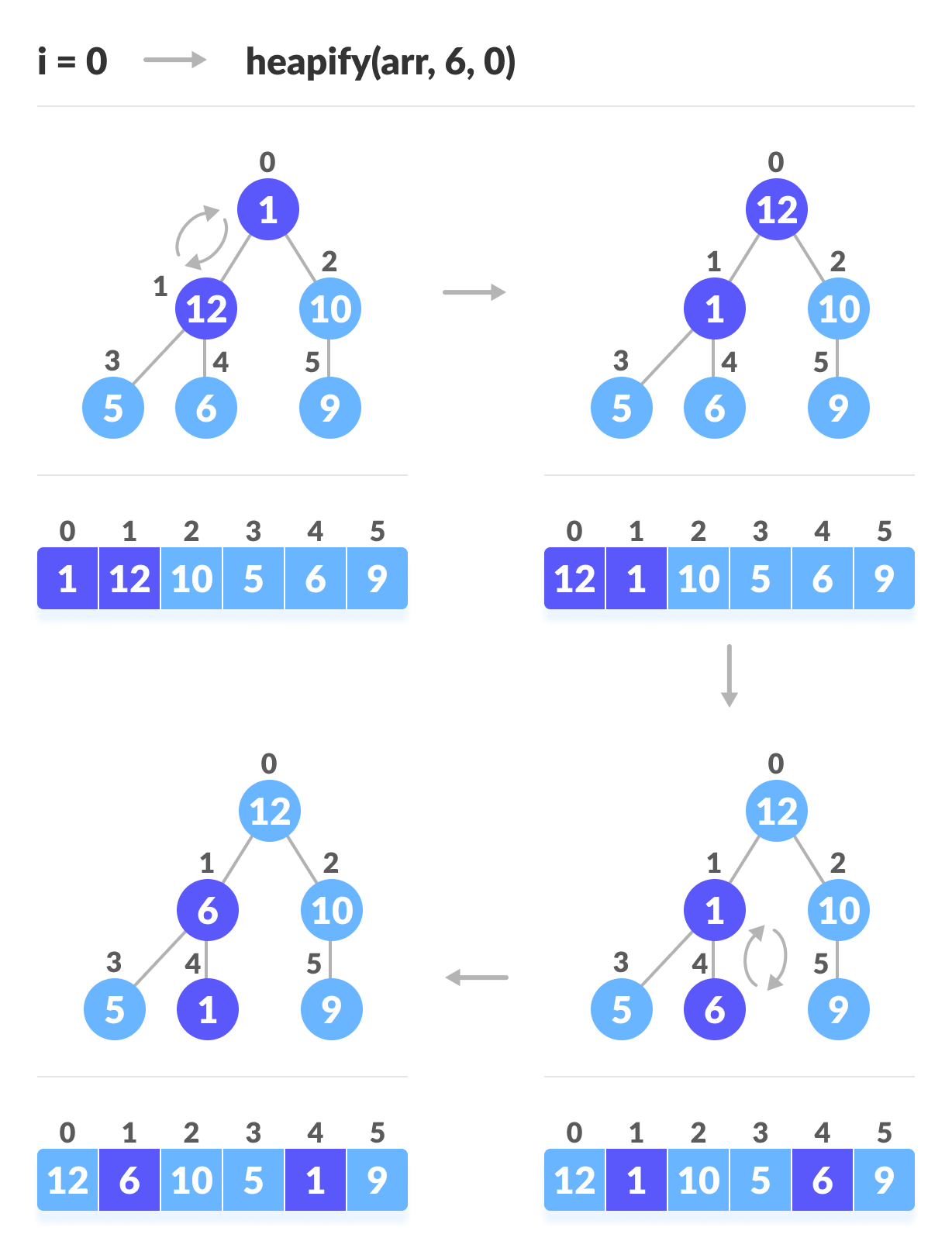
More info §

We can accomplish this task in time proportional to n*lg(n), by proceeding from left to right through the array, using swim() to ensure that the entries to the left of the scanning pointer make up a heap-ordered complete tree, like successive priority queue insertions.

A clever method that is much more efficient is to proceed from right to left, using sink() to make subheaps as we go. Every position in the array is the root of a small subheap; sink() works or such subheaps, as well. If the two children of a node are heaps, then calling sink() on that node makes the subtree rooted there a heap.